자료구조 Part2

HashTable(HashMap)

1. HashMap은 비선형 자료구조 입니다.

 

2. 일정 크기의 배열을 생성한 후에 key 값을 Hash 함수를 통하여 배열의 index 로 변환하여, 해당 index 에 해당 key값과 value 값을 저장합니다.

3. 시간 복잡도

i번째 데이터에 접근(Access) : NONE / *O(N)

-> key를 통하여 접근할 경우에는 O(1)의 시간 복잡도를 가지지만, 값을 이용하여 확인할 때는 O(N)의 시간 복잡도를 가집니다.

 

key를 통하여 접근(containsKey) : key를 hash함수를 이용하여 변환하여 해당 인덱스를 바로 조회하기 때문에 O(1) 의 시간 복잡도를 가집니다.

 

value를 통하여 접근(containsValue) : key와 달리 value 값은 hash로 변환하지 않기 때문에 특정 인덱스로 바로 이동할 수 없으며, 모든 value 값을 확인해야 하기 때문에  O(N) 의 시간 복잡도를 가집니다.

 

특정 데이터(Key)가 있는지 탐색 : O(1)

특정 데이터(Key)에 접근(Access) : O(1)

특정 데이터(Key)의 삽입/삭제 : O(1)

 

4. Hash Collision(해쉬충돌)

 

서로 다른 key 값에 대해서 Hash 함수의 반환 값이 동일한 경우를 말합니다.

 

HashMap은 무한에 가까운 key 값을 유한한 메모리에 저장해야 하기 때문에 아무리 뛰어난 Hash 로직을 사용하더라도 Hash Collision(해쉬충돌)이 발생하게 됩니다.

 

4-1. 해쉬 충돌 해결 방법

4-1-1. Open Addressing : 비어있는 다른 주소(버킷)에 데이터를 저장한다.

• 해쉬 충돌이 발생한 경우, 탐색 / 접근에 대한 시간 복잡도는 O(N)으로 증가하게 됩니다.

       -> 해당 주소로 이동 후 원하는 key 별로 value 값을 확인해야 하기 때문에 입니다.

            상기 그림을 예시로 하니를 확인하고 싶을 경우 희성-민지-하니 순으로 확인을 해야하기 때문입니다.

• 비어있는 버킷을 찾는 알고리즘은 하기와 같습니다.
• Linear Probing(선형 프로빙) -> 상기 그림
• Quadratic Probing (이차식 프로빙)
• Double Hashing (이중 해시)

4-1-2. Chaining : 해쉬 충돌이 발생한 버킷에 Linked List(Bin) 를 만들고, 해당 Linked List에 데이터를 저장한다.

Linked List로 연결할 경우 접근 / 탐색에 O(N)의 시간이 걸리므로 성능 저하가 발생하게 됩니다.

따라서 성능 저하 문제를 해결하기  위해서 BST(Binary Search Tree)를 사용할 수 있습니다.

 

 

* Java 에서는 Chaining 전략을 사용하며, 해시 충돌이 발생한 버킷에 대해 7개 Bin 까지는 Linked List, 8개 이상이 되었을 경우 BST(Red-Black Tree) 로 변경합니다.

반대의 경우 8개에서 Remove 로 인하여 Bin의 개수가 줄어들면, 6개에서 Linked List로 변경합니다.

8개 -> 7개 로 변하였을 때 바로 변경하지 않는 이유로는 잦은 변경으로 인한 자원소비를 줄일 수 있다는 장점등이 있습니다.

 

5. Load Factor : 저장할 데이터의 수 대비 너무 작은 버킷 사이즈로 인해 성능이 저하되는 것을 방지하기 위해 HashMap은 데이터가 어느 수준 이상 추가되며 , 버킷의 사이즈를 늘리고 Rehashing 을 수행합니다.

 

Java의 경우

Initial Capacity : 초기 버킷의 사이즈 : 16

Rehashing을 진행하는 데이터 양의 수준 : 버킷의 사이즈 의 75%

 

하기는 HashMap이 내부에 선언이 어떻게 되어 있는지 일부 코드를 발췌해 온 것 입니다.

    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

    static final int MAXIMUM_CAPACITY = 1 << 30;

    static final float DEFAULT_LOAD_FACTOR = 0.75f;

    static final int TREEIFY_THRESHOLD = 8;

    static final int UNTREEIFY_THRESHOLD = 6;

static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;

-> 기본 버킷의 개수는 2^4 즉 16개 입니다.

 

static final int MAXIMUM_CAPACITY = 1 << 30;

-> 최대 버킷의 개수는 2^30 즉 1,073,741,824개 입니다. 약 10억개 

 

static final float DEFAULT_LOAD_FACTOR = 0.75f;

-> Rehashing을 진행하는 데이터 양의 수준을 뜻합니다.

 

static final int TREEIFY_THRESHOLD = 8;

-> 해쉬 충돌이 일어나 버킷이 8개 이상일 때 트리화 즉 BST로 변경하는 갯수 입니다.

 

static final int UNTREEIFY_THRESHOLD = 6;

-> 해쉬 충돌이 일어나 트리화를 하였는데 노드의 개수가 6개 이하일 때, 다시 LinkedList 로 변경한다는 뜻 입니다.

 

 

Priority Queue: 우선순위 큐(Heap)

1.Priority Queue 는 비선형 자료구조이며, Heap 이라고 하는 완전 이진 트리로 구현합니다.

FIFO 인 Queue 와 다르게 데이터의 삽입 순서와 관계 없이 우선 순위가 가장 높은(낮은) 데이터를 먼저 꺼냅니다.

 

2. 용어

• 우선순위가 높은 데이터부터 꺼냄 : Max Heap (최대 힙)
• 우선순위가 낮은 데이터부터 꺼냄 : Min Heap (최소 힙)

3. 시간 복잡도

• i 번째 데이터에 접근 : None -> 데이터를 넣은 순서는 저장되어 있지 않기 때문입니다.
• 데이터의 삽입 / 삭제 : O(logN)
• Max Heap 일 때 우선순위가 가장 높은 데이터에 접근 : O(1)
• Min  Heap 일 때 우선순위가 가장 낮은 데이터에 접근 : O(1)

 

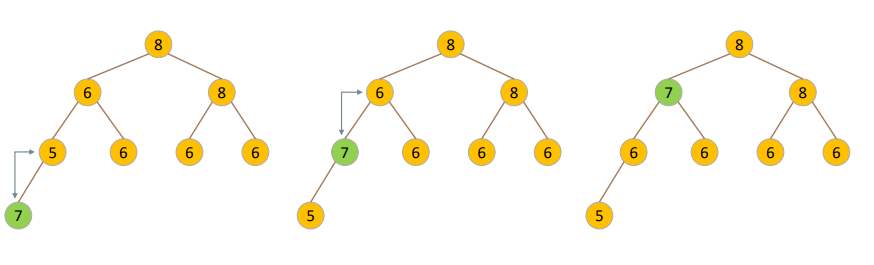
4. Max Heap 에서 데이터의 추가 과정

• Add(7)
• 시간 복잡도는 O(logN) 을 가집니다.
• 데이터를 추가할 때 완전히 정렬되는 것이 아님에 주의해야 합니다.

fun main(){
    val pq = PriorityQueue<Int>()
    pq.add(1)
    pq.add(3)
    pq.add(10)
    pq.add(5)
    pq.add(2)
    for(num in pq){
        println("num = $num")
    }
}
-----------------------------------
num = 1
num = 2
num = 10
num = 5
num = 3

 

5. Max Heap 에서 데이터의 삭제 과정

• 데이터를 poll()로 꺼낼 때 완전히 정렬이 됩니다.

import java.util.PriorityQueue

fun main(){
    val pq = PriorityQueue<Int>()
    pq.add(1)
    pq.add(3)
    pq.add(10)
    pq.add(5)
    pq.add(2)

    while(!pq.isEmpty()){
        println("num = ${pq.poll()}")
    }

}
--------------------------------------------------
num = 1
num = 2
num = 3
num = 5
num = 10

 

BST(Binary Search Tree: 이진 탐색 트리)

1. Binary Search Tree는 비선형 자료구조 이며, 논리적으로 데이터는 정렬되어 있습니다.

일반적으로 BST 는 빠른 검색을 위해 자주 사용됩니다.

 

대표적인 BST : Red-Black Tree

* 자바에서 TreeMap(TreeSet) 이  Red-Black Tree 로 구현 되어 있습니다.

MySQL Database 에서 Table 의 Index 는 B-Tree 로 되어있으며, 이는 BST 와는 다릅니다.

 

2. 정렬된 상태를 유지하면서도 데이터의  삽입/삭제를 O(logN)에 할 수 있습니다.

 

3. 시간 복잡도

• i번째 데이터에 접근 : None
• 데이터의 삽입 / 삭제 : O(logN)
• 특정 데이터에 접근 : O(logN)
• 특정 데이터 기준 Ceiling(천장) / Floor(바닥) 에 접근 : O(logN)
• ceiling(6)이라고 할 경우 7을 반환합니다. 입력 받은 값에서 위를 올려다 보았을 때
• floor(6)이라고 할 경우 5을 반환합니다. 입력 받은 값에서 아래를 쳐다보았을 때

 

 

자료 출처 : https://www.youtube.com/watch?v=wkPWWwFFBM8&feature=youtu.be

 

https://reliable-cloak-1e8.notion.site/fb0fb4eee0fc429abd36ca0806510cb6?v=e101408a85fd4f9a8a6eb1cceda9b2b0

CS 강의/스터디 (공유용)